3rd Quiz - 31/03/23

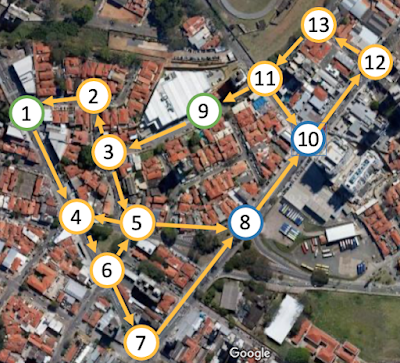
 Generally Real Networks do not behave according to the Random Networks Model, even so, they can share some properties. Analyse the following statements.

1. The degree distribution of a network can be closely aproximated as a Poisson distribution;
2. At \(\left \langle k \right \rangle\) > 1, it exists a giant component in the network;
3. Average path length can be predicted as \(\left \langle d \right \rangle = \frac{ln N}{ln \left \langle k \right \rangle}\) and can present Small World property;
4. The average clustering coefficient \(\left \langle c \right \rangle\) generally appears to be independent of the number of nodes N.

Which option contains the true statements for Random Networks that can be found also in general Real Networks?

1. I and IV;
2. II and III;
3. II and IV;
4. I, II and III;
5. None of the above.

Original idea by: Fillipi Valadares

2nd Quiz - 17/03/23

Given the image bellow of a small part of the Campinas' streets represented in a graph and your knowledge about Network Science, check the following affirmations.

1. There is only one shortest path between nodes 1 and 9 and it has length 9;
2. The given graph is strongly connected;
3. A shortest path can contain a loop;
4. If we executed BFS Algorithm starting at node 9, the longest distance would be 7;
5. The link between nodes 8 and 10 is a bridge (bridge as the Network Science definition).

Select the answer with only the true affirmations:

1. I, II and V;
2. I, III and IV;
3. II and IV;
4. II, IV and V;
5. None of the above.

Original idea by: Fillipi Valadares

1st Quiz - 10/03/23

 Given the unweighted directed graph bellow: 

What are the values for incoming and outgoing degree's of node 4, and what is the average degree of the network?

1. \(k_{4}^{in}\) = 1, \(k_{4}^{out}\) = 3, \( \left \langle k \right \rangle \) = \(\frac{6}{7}\);
2. \(k_{4}^{in}\) = 1, \(k_{4}^{out}\) = 3, \( \left \langle k \right \rangle \) = \(\frac{7}{6}\);
3. \(k_{4}^{in}\) = 3, \(k_{4}^{out}\) = 1, \( \left \langle k \right \rangle \) = \(\frac{6}{7}\);
4. \(k_{4}^{in}\) = 3, \(k_{4}^{out}\) = 1, \( \left \langle k \right \rangle \) = \(\frac{7}{6}\);
5. None of the above.

Original idea by: Fillipi Valadares